Η γραφική παράσταση συνάρτησης α βαθμού είναι ευθεία που είτε περνά από την αρχή των αξόνων (όταν έχει την μορφή ψ=α.χ όπου α σταθερός αριθμός που λέγεται συντελεστής διεύθυνσης της ευθείας και όσο πιο μεγάλος είναι τόσο πιο "απότομα"" ανεβαίνει προς τα πάνω η ευθεία μας αν α>0 και η ευθεία λέγεται αύξουσα (ή "κατεβαίνει αν α<0 οπότε η ευθεία είναι φθίνουσα).
Παρατηρείστε την γραφική παράσταση της ευθείας βάζοντας μόνιμα στην συνάρτηση β βαθμού που θα βρείτε εδώ http://phet.colorado.edu/sims/equation-grapher/equation-grapher_el.html
την τιμή 0 στα α οπότε έχετε την ευθεία y=b.x+c (που για μας στα βιβλία γράφεται ψ=α.χ+β )
οπότε αν θέσετε c=0 έχετε την πιο απλή ευθεία που είναι η ψ=b.χ και περνά απο το σημείο (0,0) .Αλλάζοντας μόνο το b δείτε τι παθαίνει η ευθεία .
Καθώς θα δίνεται στο b τιμές 1 ,μετά 2, μετά 3 θα δείτε πως αυξάνεται η κλίση της ευθείας ψ=b.χ (στο βιβλίο μας η ευθεία ονομάζεται ψ=α.χ όταν περνά από την αρχή των αξόνων καθώς για χ=0 έχουμε ψ=0 και ψ=α.χ+β όταν περνά από το σημείο (0,β) που αντιστοιχεί στο χ=0 όπου έχω ψ=β ).
Κάντε το ίδιο με το b να παίρνει αρνητικές τιμές -1, -2 και -3 τι παρατηρείτε;
Τώρα δοκιμάστε την ευθεία ψ=α.χ+β (στο phet λέγεται ψ=b.x+c )βάλτε διάφορες τιμές στα b και c αλλάζοντας μόνο ένα από αυτά π.χ το c=1 και το b = 1 και μετά 2, 3 κλπ και αντίστροφα δώστε μια τιμή στο c και αλλάξτε το b... οπότε βλέπετε τις διάφορες παραστάσεις).
Τώρα κάντε μόνοι σας (και στην συνέχεια ελέγξτε με την βοήθεια του http://phet.colorado.edu/sims/equation-grapher/equation-grapher_el.html)
τις γραφικές παραστάσεις των συναρτήσεων:
ψ=2.χ
ψ=3.χ
ψ=-2.χ
ψ=-3.χ
ψ=2.χ+4
ψ=2.χ-4
ψ=-2.χ+3
ψ=-2.χ-3
ΟΔΗΓΙΑ
Η ευθεία ορίζεται από 2 σημεία της άρα αν θέσω στο χ δυο αυθαίρετες τιμές θα βρω τα αντίστοιχα ψ π.χ στην συνάρτηση ψ=2.χ :
για χ=1 έχω ψ=2 έτσι έχουμε το σημείο (1,2)
για χ=2 έχω ψ=4 και έτσι έχουμε και το σημείο (2,4) οπότε σε ένα σύστημα ορθογωνίων αξόνων μπορούμε να κάνουμε την γραφική παράσταση εύκολα ενώνοντας τα σημεία αυτά και μεγαλώνοντας το ευθύγραμμο τμήμα και από τις 2 άκρες του.
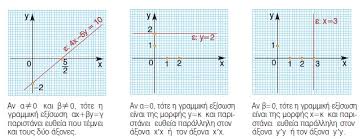
Στο σχήμα πιο πάνω η πρώτη ευθεία είναι η 4.χ-5.ψ=10 ή -5ψ=-4χ+10 ή 5ψ=4χ-10 ή ψ=4/5 χ-2 οπότε για χ=0 έχουμε ψ=-2 και για ψ=0 έχουμε 4/5 .χ =2 ή χ=5/2 και έτσι η ευθεία μας περνά απο τα σημεία (0,-2) και (5/2,0).
Στην δεύτερη ευθεία για κάθε χ έχουμε ψ=2 άρα είναι οριζόντια η ευθεία όπως στο 2ο σχήμα και στην τρίτη ευθεία το χ=3 πάντα άρα είναι κατακόρυφη η ευθεία όπως στο 30 σχήμα..
Δείτε ακόμη :1. http://el.wikipedia.org/wiki/%CE%95%CF%85%CE%B8%CE%B5%CE%AF%CE%B1
2. http://el.wikipedia.org/wiki/%CE%95%CE%BE%CE%AF%CF%83%CF%89%CF%83%CE%B7_%CE%B5%CF%85%CE%B8%CE%B5%CE%AF%CE%B1%CF%82
3.http://users.sch.gr/gkaripid/theory/b%20lik/meth%20efthia.pdf
Παρατηρείστε την γραφική παράσταση της ευθείας βάζοντας μόνιμα στην συνάρτηση β βαθμού που θα βρείτε εδώ http://phet.colorado.edu/sims/equation-grapher/equation-grapher_el.html
την τιμή 0 στα α οπότε έχετε την ευθεία y=b.x+c (που για μας στα βιβλία γράφεται ψ=α.χ+β )
οπότε αν θέσετε c=0 έχετε την πιο απλή ευθεία που είναι η ψ=b.χ και περνά απο το σημείο (0,0) .Αλλάζοντας μόνο το b δείτε τι παθαίνει η ευθεία .
Καθώς θα δίνεται στο b τιμές 1 ,μετά 2, μετά 3 θα δείτε πως αυξάνεται η κλίση της ευθείας ψ=b.χ (στο βιβλίο μας η ευθεία ονομάζεται ψ=α.χ όταν περνά από την αρχή των αξόνων καθώς για χ=0 έχουμε ψ=0 και ψ=α.χ+β όταν περνά από το σημείο (0,β) που αντιστοιχεί στο χ=0 όπου έχω ψ=β ).
Κάντε το ίδιο με το b να παίρνει αρνητικές τιμές -1, -2 και -3 τι παρατηρείτε;
Τώρα δοκιμάστε την ευθεία ψ=α.χ+β (στο phet λέγεται ψ=b.x+c )βάλτε διάφορες τιμές στα b και c αλλάζοντας μόνο ένα από αυτά π.χ το c=1 και το b = 1 και μετά 2, 3 κλπ και αντίστροφα δώστε μια τιμή στο c και αλλάξτε το b... οπότε βλέπετε τις διάφορες παραστάσεις).
Τώρα κάντε μόνοι σας (και στην συνέχεια ελέγξτε με την βοήθεια του http://phet.colorado.edu/sims/equation-grapher/equation-grapher_el.html)
τις γραφικές παραστάσεις των συναρτήσεων:
ψ=2.χ
ψ=3.χ
ψ=-2.χ
ψ=-3.χ
ψ=2.χ+4
ψ=2.χ-4
ψ=-2.χ+3
ψ=-2.χ-3
ΟΔΗΓΙΑ
Η ευθεία ορίζεται από 2 σημεία της άρα αν θέσω στο χ δυο αυθαίρετες τιμές θα βρω τα αντίστοιχα ψ π.χ στην συνάρτηση ψ=2.χ :
για χ=1 έχω ψ=2 έτσι έχουμε το σημείο (1,2)
για χ=2 έχω ψ=4 και έτσι έχουμε και το σημείο (2,4) οπότε σε ένα σύστημα ορθογωνίων αξόνων μπορούμε να κάνουμε την γραφική παράσταση εύκολα ενώνοντας τα σημεία αυτά και μεγαλώνοντας το ευθύγραμμο τμήμα και από τις 2 άκρες του.
Στο σχήμα πιο πάνω η πρώτη ευθεία είναι η 4.χ-5.ψ=10 ή -5ψ=-4χ+10 ή 5ψ=4χ-10 ή ψ=4/5 χ-2 οπότε για χ=0 έχουμε ψ=-2 και για ψ=0 έχουμε 4/5 .χ =2 ή χ=5/2 και έτσι η ευθεία μας περνά απο τα σημεία (0,-2) και (5/2,0).
Στην δεύτερη ευθεία για κάθε χ έχουμε ψ=2 άρα είναι οριζόντια η ευθεία όπως στο 2ο σχήμα και στην τρίτη ευθεία το χ=3 πάντα άρα είναι κατακόρυφη η ευθεία όπως στο 30 σχήμα..
Δείτε ακόμη :1. http://el.wikipedia.org/wiki/%CE%95%CF%85%CE%B8%CE%B5%CE%AF%CE%B1
2. http://el.wikipedia.org/wiki/%CE%95%CE%BE%CE%AF%CF%83%CF%89%CF%83%CE%B7_%CE%B5%CF%85%CE%B8%CE%B5%CE%AF%CE%B1%CF%82
3.http://users.sch.gr/gkaripid/theory/b%20lik/meth%20efthia.pdf
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου